斐波那契数列(Fibonacci sequence)的6种解法

算法 阅读量

　　最近在刷Leetcode，目前在“Explore”中出了很多学习和面试的专题，刷了几个系列感觉非常不错。“斐波那契数列”是一个很经典的问题了，无论是讲解递归还是动态规划的文章中都时常能看到。可以用斐波那契数列求解的题目也有很多，比如“爬梯子”和“兔子繁殖”等经典问题。在此主要是记录一下解决“斐波那契数列”类似问题的6种思路。

版权声明：本文为博主原创文章，未经博主允许不得转载。

本篇文章中的所有事例在我的github中均有完整的代码实现，链接为：https://github.com/ten-z/Fibonacci-Sequence

0. 前言

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……
在数学上，斐波纳契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3，n∈N*)。

百度百科中关于斐波那契数列的描述

一般斐波那契数列相关的问题都是给出n求F(n)，下面解法也都是针对这种题型来的。

1. 方法一：递归/回溯/暴力解法（Recursion）

由于斐波那契数列有很明确的递归关系(F(n)=F(n-1)+F(n-2)(n>=3，n∈N*))和递归终止条件(F(0)=0， F(1)=1，有的会用F(2)=1)。因此，很容易用递归暴力解决。

越抽象的问题用图来说明会比较容易理解，下面以计算f(4)为例，计算f(4)递归执行树如下图：

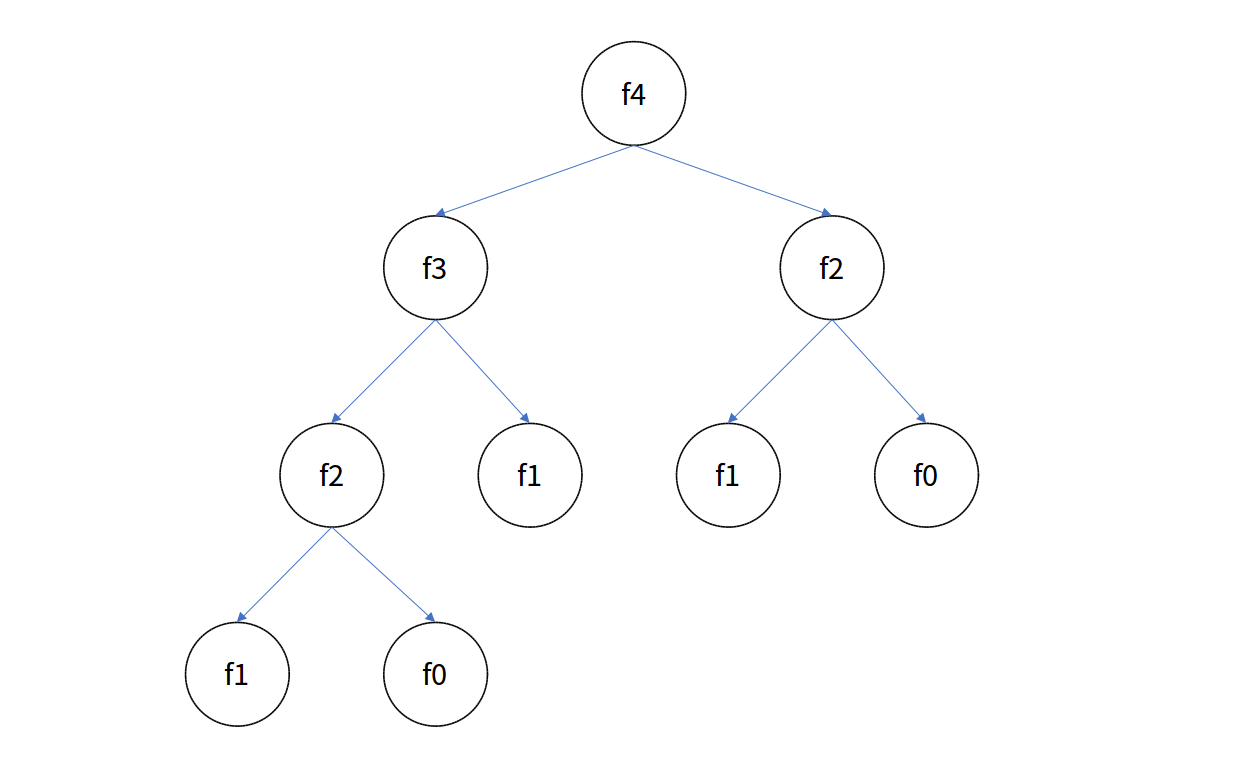
通过这个图以及递归关系很容易看出，递归的逻辑是：要求f(n)，就要先求出f(n-1)和f(n-2)的值；而求f(n-1)，又要先求出f(n-2)和f(n-3)的值，这样一步一步往前寻找，直到找到f(1)=1和f(2)=1为止。具体代码实现如下：

递归解法
1
2
3
4
5
6
7
public static int fibonacci(int n) {
  if (n < 2) {
    return n;
  } else {
    return fibonacci(n-1) + fibonacci(n-2);
  }
}

时间复杂度：$O(2^n)$
空间复杂度：$O(n)$

2. 方法二：记忆化搜索（Recursion with Memoization）

记忆化搜索本质是对递归算法的剪枝优化。还是以计算f(4)为例，下图为计算f(4)的递归执行树，可以看出求解f(4)时存在着大量的重复计算：

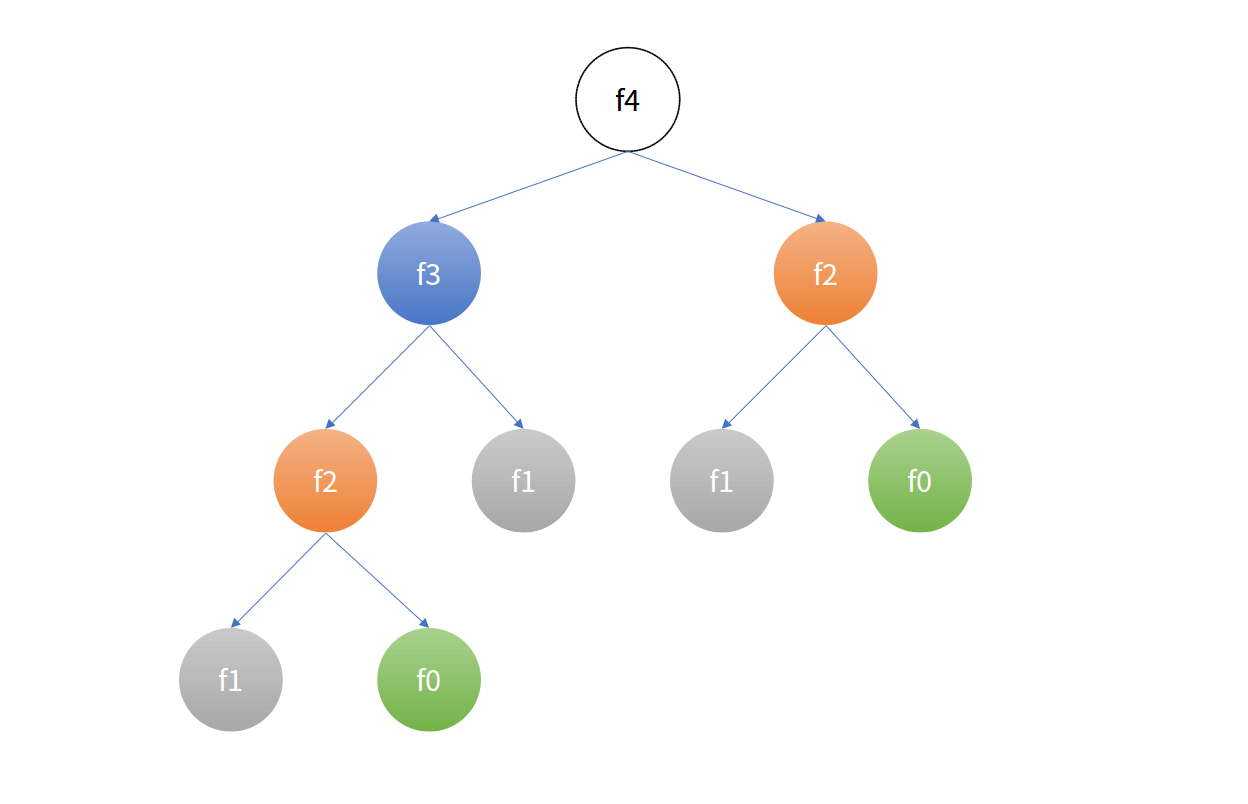
为了解决这些重复计算，可以将第一次求出的结果存储起来，一般来讲是按下标存放在memo数组中。下次计算前先去数组相应位置查找，如果有结果，就可直接返回，避免重复的计算。
代码也很简单：

记忆化搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
 public static int fibonacci(int n) {
	if(n<2)return n;

	//初始化memo数组,从1～n，所以长度为n+1
	int[] memo = new int[n+1];
	return fibonacciMemorize(n, memo);
}
	
//用memo数组存储计算结果
public static int fibonacciMemorize(int n, int[] memo) {
	if(n==1 || n==2){
		return 1;
	}
 
	//如果memo(n)有值，直接返回memo[n]，减少递归次数，由于n从1开始，memo[0]=0不受影响。
	if(memo[n]==0){
		//如果当前f(n)没被计算过，则计算后将结果存入memo[n]
		memo[n] = fibonacciMemorize(n-1, memo) + fibonacciMemorize(n-2, memo);
	}
	return memo[n];
}

时间复杂度：$O(n)$
空间复杂度：$O(n)$

3. 方法三：动态规划（Dynamic Programming）

根据动态规划的定义，由于这个问题可以分解成子问题，它包含了子问题的最优性质，即它的最优解可以从子问题的最优解中有效地构造出来。因此我们可以用动态规划来解决这个问题。

不过定义理解起来有点复杂，其实动态规划的解法可以看作是记忆化搜索思想的逆向思路。可以自行先打印下方法二中memo数组赋值的顺序，可以发现：memo数组是从memo[1]，memo[2],memo[3]…memo[n]依次赋值的，每一位置的值为前两个位置值的和。而memo[n]就是我们要求的f(n)。所以可见，如果抛弃递归的思路，仅在数组中用循环也可以依次计算数出组中的值，最后求得f(n)。具体点说，就是由于memo[1]=1和memo[2]=1可知，所以可以先算出memo[3] = memo[2] + memo[1],然后memo[4] = memo[3]+memo[2]…,直到求出memo[n]。而memo[n]就是要求的f(n)。

总结一下：递归和记忆化搜索的思路是：求f(n),要先求出f(n-1)和f(n-2)的值；而求f(n-1)，又要先求出f(n-2)和f(n-3)的值，这样一步一步往前寻找，直到找到f(1)=1和f(2)=1为止。
而动态规划的思路是：求f(n)，由于我们已经知道f(1) = 1,f(2) = 1，所以可以先求出f(3) = f(1) + f(2)，再求f(4)…这样一步一步从前向后直到求出f(n)。

代码如下：

动态规划，用循环代替了递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static int fibonacciDynamic(int n) {
       if (n < 2) {
           return n;
       }

//初始化memo数组,从1～n，所以长度为n+1
       int[] memo = new int[n + 1];

//已知的0和1位置的值，代替递归终止条件。
       memo[0] = 0;
       memo[1] = 1;
	
       for (int i = 2; i <= n; i++) {
           memo[i] = memo[i - 1] + memo[i - 2];
       }
//memo[n]即f(n)的值
       return memo[n];
   }

时间复杂度：$O(n)$
空间复杂度：$O(n)$

4. 方法四：斐波那契数（Fibonacci Number）

这个方法本质是对方法三在空间复杂度上的优化。在动态规划的解法中，我们用了一个长度为n+1的memo数组来辅助计算f(n)，但是其实f(n)的值只跟f(n-1)和f(n-2)两个数有关，那么前面的n+1-3个数据能不能优化呢？

斐波那契数这个方法就是通过两个索引来代替memo数组，在每次循环之后更新两个索引的值，这样可以使空间复杂度降低至$O(1)$的级别。

废话不多说，上代码：

斐波那契数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 public static int fibonacciNumber(int n) {
       if (n < 2) {
           return n;
       }

//用first和second存储每次的memo[n-1]和memo[n-2],不断更新first和second的值，代替memo数组
       int first = 0;
       int second = 1;
       for (int i = 2; i <= n; i++) {
           int third = first + second;
           first = second;
           second = third;
       }

//最后一次循环交换后，f(n)==second
       return second;
   }

时间复杂度：$O(n)$
空间复杂度：$O(1)$

斐波那契数列的常规方法主要就是上面四种，经过一步一步的优化，将时间复杂度降至O(n)，空间复杂度降至O(1)。后面介绍的两种特（qi）殊（pa）方法主要是针对时间复杂度的优化。

5. 方法五：矩阵法（Binets Method）

矩阵法的本质是将斐波那契数列问题转化为指数计算的问题，而求解例如Q的n次方的问题可以很容易的使用二分法的思路，将时间复杂度降为$O(logn)$。
先看一下矩阵的乘法计算：
已知:
$$A=\left[\begin{matrix}a & b\\c & d\end{matrix}\right],
B=\left[\begin{matrix}e\\f\end{matrix}\right]$$
所以：
$$AB=\left[\begin{matrix}ae+bf\\ce+df\end{matrix}\right]
$$
反之亦然。

根据上面的规则，可以将斐波那次数列作如下改动：

$$\left[\begin{matrix}f(n)\\f(n-1)\end{matrix}\right]
=\left[\begin{matrix}f(n-1)+f(n-2)\\f(n-1)\end{matrix}\right]
=\left[\begin{matrix}f(n-1)×1+f(n-2)×1\\f(n-1)×1+f(n-2)×0\end{matrix}\right]
=\left[\begin{matrix}1&1\\1&0\end{matrix}\right]
×\left[\begin{matrix}f(n-1)\\f(n-2)\end{matrix}\right]$$

$$=….=\left[\begin{matrix}1&1\\1&0\end{matrix}\right]^{n-1}
×\left[\begin{matrix}f(1)\\f(0)\end{matrix}\right]
=\left[\begin{matrix}1&1\\1&0\end{matrix}\right]^{n-1}
×\left[\begin{matrix}1\\0\end{matrix}\right]$$

如果记$Q=\left[\begin{matrix}1&1\\1&0\end{matrix}\right]$，那么
$$\left[\begin{matrix}f(n)\\f(n-1)\end{matrix}\right]
=Q^{n-1}×\left[\begin{matrix}1\\0\end{matrix}\right]
$$
由于乘数是$\left[\begin{matrix}1\\0\end{matrix}\right]$，所以f(n)的值就是计算出$Q^{n-1}$的矩阵后最左上角那一位的值。

如此，斐波那契数列就转换为了求Q的n-1次方的问题。

求解$Q^{n-1}$的问题最主要的思路就是二分法，将指数n每次二分，根据当前n的奇偶不断递归，偶数就直接除以2，并将结果自己乘自己；奇数因为除不尽，结果还得再多乘一次Q。
当然，这里的乘法也是矩阵乘法，需要自己写出相应的方法。
示意图如下：

下面是具体代码：

矩阵法--指数二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

   public static int fibonacci(int n, int[][] q) {
       if(n<2)return n;
       int[][] res = powRecursion(n-1, q);
       return res[0][0];
   }
   //递归实现的pow()，每次将指数二分
   public static int[][] powRecursion(int n, int[][] q) {
       if(n == 1)return q;
//每次指数/2
       int[][] r = powRecursion(n>>1, q);
//奇数的话要多乘一个底数，偶数则不用
       if ((n & 1) == 1){
           return multiply(multiply(r,r), q);
       }else{
           return multiply(r,r);
       }
   }

   //矩阵乘法的实现
   public static int[][] multiply(int[][] a, int[][] b) {
       int[][] c = new int[2][2];
       for (int i = 0; i < 2; i++) {
           for (int j = 0; j < 2; j++) {
               c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
           }
       }
       return c;
   }

对于求解$Q^{n-1}$，或者说普遍求解$Q^{n}$这类问题，除了上面比较容易理解的递归之外，还可以利用二进制的一些技巧，将指数进行二进制的拆解。举个例子：

假设求：$Q^{11}$。我们已知11=1011=1000+0010+0001(拆解成二进制的和)
所以$$Q^{11}=Q^{8+2+1}=Q^8×Q^2×Q^1=Q^{2^3}×Q^{2^1}×Q^{2^0}$$

也就是说，将11转换成二进制，为1的位置就是底数要乘的位置，而由于二进制出现在幂的位置上，所以反应在Q上就变成前一位乘积的平方的关系。

逻辑稍有点复杂，还是上面的例子，为方便发现规律，假设Q = 3：
$$3^{0001}=3$$
$$3^{0010}= 3×3 = 9$$
$$3^{0100} = 9×9 = 81$$
$$3^{1000} = 81×81 = 6561$$
所以：
$$3^{1011} = 3×9×6561 = 177147$$

具体执行逻辑为：将指数转换成二进制后，从右向左查看二进制每一位是否为1，如上所示，第一位为1，那么最终结果乘上$3^1$；继续看第二位，此时不用再计算$3^2$，直接将上一位（第一位）的结果自乘一下就是第二位的结果。同时由于第二位为1，最终结果也乘上第二位算出的结果；继续看第三位，也是一样的先计算出第三位的结果，由于第三位等于0，那么最终结果不乘入；到第四位，根据第三位的结果自乘算出第四位的结果，第四位是1，将第四位乘入最终结果。

写成代码就是如下的逻辑：

矩阵法--指数二进制拆分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
   public static int[][] powBinary(int n, int[][] a) {
//初始化矩阵,示意写法
       int[][] ret = {[1, 0}], [0, 1]};
       while (n > 0) {
           if ((n & 1) == 1) {
	//二进制中1的位置需要乘入结果，其结果等于低（前）一位结果的平方
               ret = multiply(ret, a);
           }
    //右移，看二进制指数高一位是否为1
           n >>= 1;
    //无论高一位是否为1，都先算出结果，等于当前结果的平方
           a = multiply(a, a);
       }
       return ret;
   }

注意：两种方法调用的时候是n-1：因为是$Q^{n-1}$。

时间复杂度：$O(logn)$
空间复杂度：$O(1)$

6. 方法六：公式法（Fibonacci Formula）

先给出第n项斐波那契数列f(n)的通项公式:
$$F_n=1/\sqrt{5}{\Bigl[
\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n-
\Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n
\Bigr]}$$

Leetcode里给出的标准的推导方法是：
由于F(n+2) = F(n+1) + F(n)，假设$$F_n=a^n$$
可以得到：
$$a^{n+2}=a^{n+1}+a^n$$
简化下可得$a^{2}-a-1=0$,
这样a的解就是:$$a=\frac{1\pm\sqrt{5}}{2}$$
所以f(n)的通解为:
$$F_n=A\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n+B\Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n$$

由于又知道两个特殊值：$f(0)=0;f(1)=1$，带入公式中可求出：
$$A=\frac{1}{\sqrt{5}}$$
$$B=-A=-\frac{1}{\sqrt{5}}$$

带入通项公式，可得：
$$F_n=1/\sqrt{5}{\Bigl[
\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n-
\Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n
\Bigr]}$$

代码反而很简单：

通项公式
1
2
3
4
5
6
7
8
9
   public static int fibonacci(int n) {
if(n < 2)
	return n;
	
double sqrt5=Math.sqrt(5);
       double fibn=Math.pow((1+sqrt5)/2,n)-Math.pow((1-sqrt5)/2,n);
       return (int)(fibn/sqrt5);
   }

时间复杂度：$O(logn)$–Math.pow()方法需要
空间复杂度：$O(1)$

7. 总结

　　斐波那契数列的六种解法基本如上，后两种方法为了达到$O(logn)$级别的时间复杂度可谓是“不择手段”。多写两句，最近在刷算法题和复习基本的东西，感觉基础的东西确实需要好好看看。之前业务压力太大，甭说博客了，简单的总结时间都没有，睡眠也不太够。趁着最近调整调整，博客也要及时更新了。没有什么事情是很容易的，继续加油吧。

Powered by Hexo and Hexo-theme-hiker

Copyright © 2018 - 2023 TEN-Z'S BLOG All Rights Reserved.

访客数 : | 访问量 :